
Positioning is about finding the best way to utilize sensor measurements which are often quite erroneous. How does mathematics help with this?
I recently finished my master’s thesis on vehicle positioning. In this blog post, I’m going to describe in simple terms what is mathematics used for in positioning algorithms. The purpose is not to focus on the mathematics itself, but on why it is used. After all, math can be quite complicated, so there should be a good reason for making use of it. In this text, I’m concentrating on university-level mathematics: probability theory, linear algebra & mathematical optimization.
Factoring in uncertainty with probability theory
Positioning is based on measurements from different sensors, and these measurements are always erroneous to some extent. For instance, position measurements from GPS (or more generally, GNSS) are rarely very accurate, and often their uncertainty also varies from one moment to another. The more clearly the GPS receiver can detect the signals sent by the GPS satellites, the more accurate the position measurements on average are.
By means of probability theory, the inherent uncertainty of measurements can be taken into account. In practice this means that the measurements are modelled as random variables, and quantities usually describing randomness, such as standard deviation or variance, are used for describing uncertainty. By doing this, the formulas of probability theory can be applied to weight measurements according to their uncertainty. For instance, a highly uncertain GPS position measurement can be given less weight in the computations than a more reliable position measurement.
Moreover, when the quantity being estimated is also modelled as a random variable, probability theory makes it possible to estimate the uncertainty of the estimate itself. With position, such an uncertainty estimate could for example be that the position estimate produced by the algorithm is off by at most 1 meter with 95 % probability.
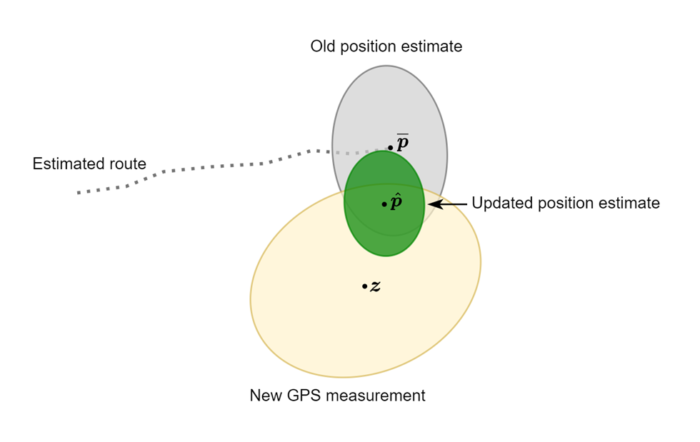
Figure 1 illustrates uncertainties and their use in position estimation. In this figure, the vehicle has travelled from left to right, and before processing the new GPS measurement, the vehicle is estimated to be at position However, this estimate includes some uncertainty, which is depicted by the grey ellipse: the true position is estimated to be somewhere within the grey ellipse with 95 % probability.
The uncertainty of the new GPS measurement is depicted by the yellow ellipse. This ellipse is larger than the grey one, since the GPS measurement is more uncertain than the existing position estimate. In processing the new GPS measurement, the updated position estimate
is computed as a compromise between the old estimate and the GPS measurement, with both being weighted according to their uncertainties. Since the old estimate is less uncertain, the updated estimate is closer to it than to the GPS measurement. The green ellipse depicts the uncertainty of the updated estimate.
Plenty of use for linear algebra
Quantities in positioning are often multidimensional, and since matrices are the standard tool for working with multidimensional data, they are used extensively in positioning. One use case for matrices that I personally find interesting is the transformation of multidimensional measurements between different coordinate frames. A typical example of this is the handling of angular velocity measurements from an inertial measurement unit, which we shall dive into next.
The inertial measurement unit (IMU) is a sensor mounted on the vehicle which measures the vehicle’s angular velocity. The angular velocity measurements are three-dimensional vectors. The components of these vectors are the scalar angular velocities of the vehicle with respect to the x-, y-, and z-axis of the IMU’s coordinate frame. In positioning, however, we are primarily interested in angular velocity with respect to the axes of the vehicle’s coordinate frame. These two coordinate frames might not always be aligned: often their orientation differs by some known rotation. With specific types of matrices, called rotation matrices, the angular velocity measurements can be easily transformed from the IMU’s coordinate frame to the vehicle’s coordinate frame.
Matrix computations are also useful since computers perform them relatively fast. This means that if a computational problem can be converted to a problem of numerical linear algebra, solving it may speed up significantly. In positioning this is relevant especially when estimates need to be produced in real-time.
Selecting the best alternative with optimization
Sometimes it is necessary to select one out of a countless number of (numerical) alternatives. If the quality of the different alternatives can be expressed with a numerical formula, methods of mathematical optimization can be used to find the best alternative in terms of this formula (e.g., the alternative that maximizes the value of the formula). In the positioning algorithm we have developed, this kind of an approach is used in estimating the vehicle’s heading.
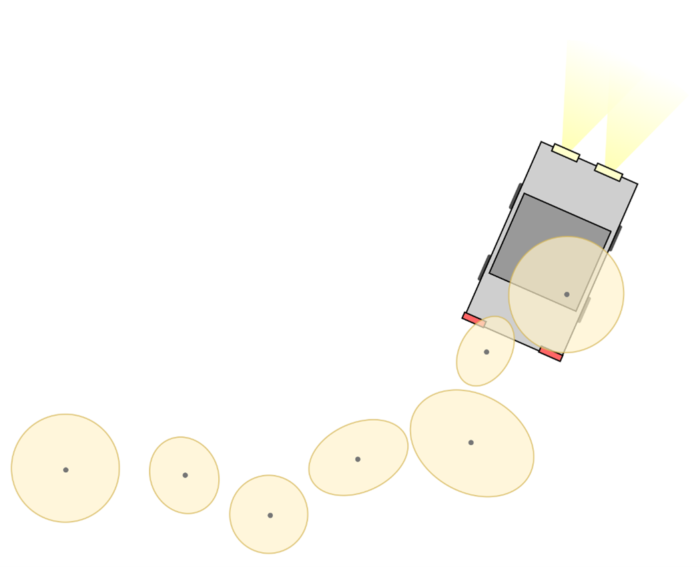
The basic setup of the heading estimation is illustrated in Figure 2. The figure shows a vehicle and a few recent GPS measurements from the middle point of the moving vehicle. The GPS measurements are somewhat noisy, but shape of the vehicle’s route is still clearly visible: the vehicle has travelled from left to right while also turning up.
How could a computer automatically determine the current heading of the vehicle by utilizing the recent GPS measurements? In the algorithm we have developed, mathematical optimization plays a key role in solving this problem.

Olli Huopio
Software Developer
I work as a software designer at Atostek. I joined the company in the summer of 2021, and graduated from Aalto University in late 2022. My studies focused on applied mathematics and computer science, and I aim to continue with these compelling subjects in my career as well.