Mihin paikannusalgoritmissa tarvitaan matematiikkaa?

Paikannuslaskennassa haasteena on hyödyntää mittausanturien epätarkkoja mittauksia parhaalla mahdollisella tavalla. Miten matematiikka tässä auttaa?

Sain äskettäin valmiiksi diplomityöni, joka käsittelee ajoneuvon paikantamista. Tässä kirjoituksessa avaan yleistajuisesti asiasta kiinnostuneille sitä, mihin matematiikkaa paikannusalgoritmissa käytetään. Pääroolissa ei siis ole matematiikka itsessään, vaan sen käyttötarkoitukset – mitä monimutkaisen matemaattisen koneiston käytöllä saavutetaan? Keskityn kirjoituksessa korkeakoulutasoiseen matematiikkaan, tarkemmin sanottuna todennäköisyys- ja matriisilaskentaan sekä matemaattiseen optimointiin.

Todennäköisyyslaskennalla epävarmuudet huomioon

Paikantaminen perustuu mittalaitteista saataville mittauksille, jotka luonnollisesti sisältävät aina jonkin verran virhettä. Esimerkiksi GPS-paikkamittaukset (yleisemmin GNSS-paikkamittaukset) ovat harvoin täysin tarkkoja, ja niiden epävarmuus yleensä myös vaihtelee hetkestä toiseen. Mitä selkeämpinä GPS-vastaanotin havaitsee satelliittien lähettämät paikannussignaalit, sitä tarkempi paikkamittaus keskimäärin on.

Todennäköisyyslaskenta tarjoaa keinoja mittausten epävarmuuden ja sen vaihtelun huomioimiseen. Käytännössä tämä tarkoittaa sitä, että mittauksia käsitellään (“mallinnetaan”) satunnaismuuttujina ja satunnaisuutta kuvaavia suureita, kuten keskihajontaa ja varianssia, käytetään kuvaamaan epävarmuutta. Tällöin todennäköisyyslaskentaa soveltaen mittauksia voidaan painottaa niiden epävarmuuden mukaan. Esimerkiksi paikan estimoinnissa hyvin epävarmalle GPS-mittaukselle voidaan antaa vähemmän painoarvoa kuin luotettavammalle mittaukselle.

Lisäksi, kun itse estimoitavaa suuretta käsitellään satunnaismuuttujana, todennäköisyyslaskennalla saadaan tuotettua arvioita myös laskettujen estimaattien epävarmuudesta. Paikan suhteen tällainen epävarmuusarvio voisi esimerkiksi olla, että algoritmin tuottama paikkaestimaatti on 95 prosentin todennäköisyydellä enintään metrin pielessä.

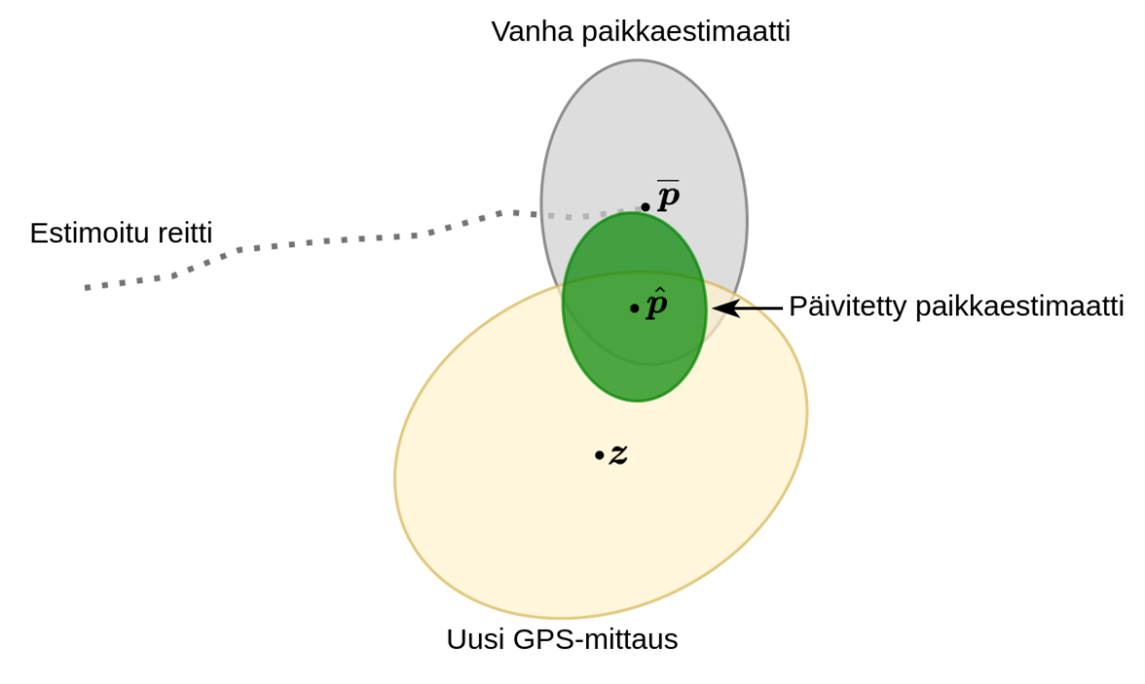
Kuvassa 1 havainnollistetaan epävarmuuksia ja niiden käyttöä paikan estimoinnissa. Ajoneuvo on liikkunut kuvassa vasemmalta oikealle ja ennen uuden GPS-mittauksen huomioimista ajoneuvon arvellaan olevan pisteessä  Tähän estimaattiin liittyy kuitenkin epävarmuutta, jota kuvastaa harmaa ellipsi: oikean paikan arvellaan olevan 95 prosentin todennäköisyydellä jossakin harmaan ellipsin sisäpuolella.

Uuden GPS-mittauksen epävarmuutta kuvastaa keltainen ellipsi, joka on harmaata suurempi, sillä mittaukseen liittyy enemmän epävarmuutta kuin senhetkiseen estimaattiin. Uusi, päivitetty estimaatti lasketaan vanhan estimaatin ja GPS-mittauksen välisenä kompromissina, jossa kumpaakin painotetaan niiden epävarmuuksien mukaisesti. Koska vanhaan estimaattiin liittyy suhteessa vähemmän epävarmuutta, uusi estimaatti on lähempänä vanhaa estimaattia kuin GPS-mittausta. Vihreä ellipsi kuvastaa tähän uuteen estimaattiin liittyvää epävarmuutta.

Matriisilaskenta monessa mukana

Paikannuksessa käsiteltävät suureet ovat usein moniulotteisia, ja matriisit ovat moniulotteisen laskennan peruskauraa. Eräs mielestäni mielenkiintoinen käyttökohde matriiseille paikannuksessa on moniulotteisten mittausten muuntaminen koordinaatistosta toiseen. Tyyppiesimerkkinä tästä toimii inertia-anturin mittausten käsittely, josta hiukan tarkemmin seuraavaksi.

Ajoneuvon kyydissä oleva inertia-anturi mittaa ajoneuvon kulmanopeutta. Nämä kulmanopeusmittaukset ovat kolmiulotteisia vektoreita, jotka koostuvat skalaarisista kulmanopeuksista anturin oman koordinaatiston x-, y- ja z-akselien suhteen. Paikannuslaskuissa ollaan kuitenkin lähtökohtaisesti kiinnostuneita kulmanopeuksista ajoneuvon oman koordinaatiston akselien suhteen, eivätkä anturin ja ajoneuvon koordinaatistot aina ole linjassa keskenään: usein ne eroavat toisistaan tietyn kiertoliikkeen verran. Niin sanotuilla kiertomatriiseilla kulmanopeusmittaukset saadaan kätevästi muunnettua anturin koordinaatistosta ajoneuvon koordinaatistoon.

Matriisilaskenta on hyödyllistä myös siinä mielessä, että se on tietokoneella yleensä nopeaa. Eli jos jokin laskentaongelma saadaan puettua matriisimuotoon, sen ratkaiseminen voi nopeutua hyvinkin huomattavasti. Paikannuksessa tämä on tärkeää etenkin silloin, kun estimaatteja halutaan tuottaa reaaliaikaisesti.

Optimoinnilla löydetään paras vaihtoehto monesta

Joskus on valittava lukemattomista eri (numeerisista) vaihtoehdoista yksi. Jos eri vaihtoehtojen ”hyvyyttä” voi ilmaista numeerisella lausekkeella, matemaattisen optimoinnin keinoilla on mahdollista löytää se vaihtoehto, joka on lausekkeen mittarin mukaan paras (esimerkiksi tuottaa suurimman arvon lausekkeelle). Kehittämässämme paikannusalgoritmissa tällaista lähestymistapaa käytetään ajoneuvon suuntakulman estimointiin.

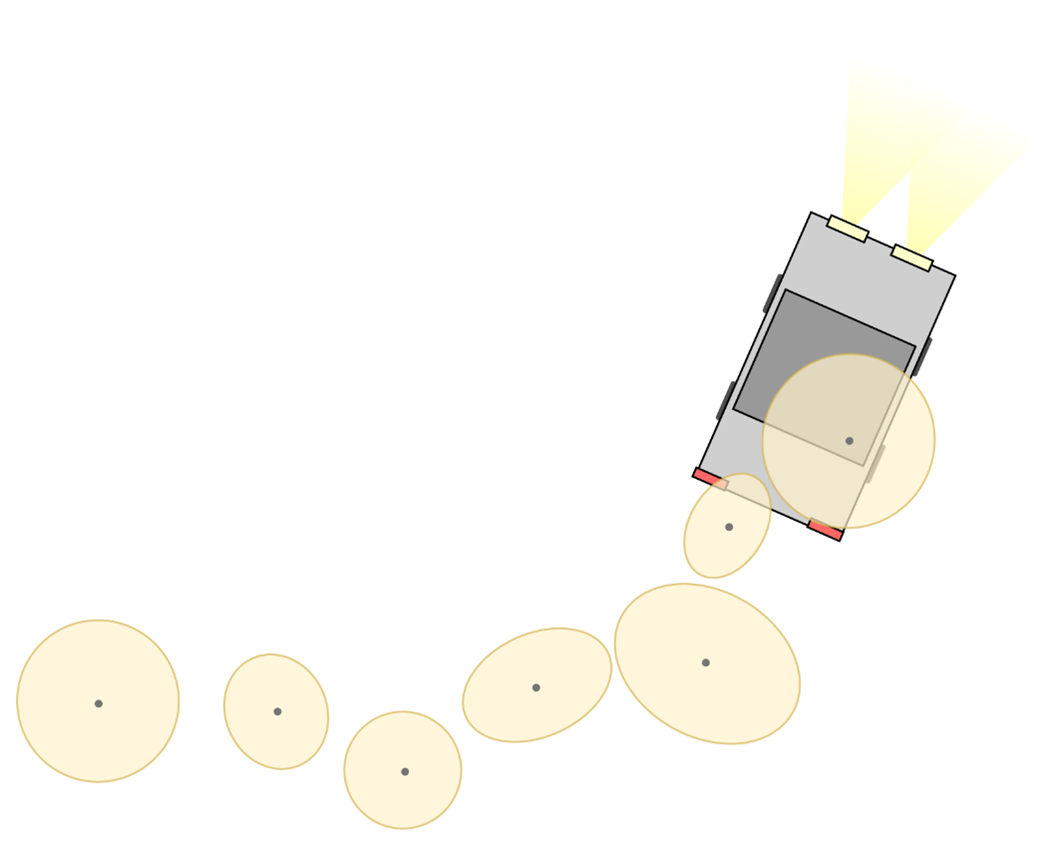
Suuntakulman estimoinnin perusasetelmaa havainnollistetaan kuvassa 2. Kuvassa on ajoneuvo sekä muutama viimeaikainen GPS-mittaus liikkuvan ajoneuvon keskipisteestä. GPS-mittaukset ovat kohinaisia, mutta niistä on kuitenkin nähtävissä ajoneuvon reitin muoto: ajoneuvo on tullut vasemmalta ja kaartanut sen jälkeen ylöspäin.

Miten tietokone voisi näitä GPS-mittauksia käyttäen päätellä tarkasti ajoneuvon nykyisen suuntakulman? Kehittämässämme algoritmissa matemaattisella optimoinnilla on keskeinen rooli tämän probleeman ratkaisussa.

Olli Huopio
Ohjelmistosuunnittelija

Työskentelen Atostekilla ohjelmistosuunnittelijana. Olen aloittanut atostekilaisena vuoden 2021 kesällä, ja valmistuin Aalto-yliopistosta vuoden 2022 lopussa. Opinnoissani keskityin soveltavaan matematiikkaan ja tietotekniikkaan. Näiden aiheiden leikkauskohdassa pyrin jatkamaan myös työelämässä.